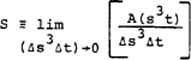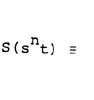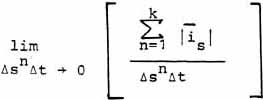|
-- SCALARS AND VECTORS HAVE SUBSTRUCTURES --
As can now be seen, the sum of each structure in figure 13 is observably
zero. Therefore we might define the sum as a "zero spatial
vector." We note, however, that it actually exists for a time
Δt and is thus a spatiotemporal entity,
rigorously.
If we
define the internal stress action A in a region Δs3Δt
of spacetime as
|
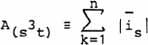
|
(29) |
and the 4-space internal stress intensity or potential
as
|
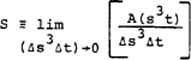
|
(30) |
where 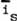 is any internal vector in the substructure, Δs3
is the spatial volume (about a point) containing vector
is any internal vector in the substructure, Δs3
is the spatial volume (about a point) containing vector  ,
and Δt is the inseparable time during which
these component actions occurred, then we see that, stress-wise, all the
"zero-vectors" in figure 13 are quite different in their
internal stresses, 4-space potentials, and internal substructures.
For the five "zero sum" vectors, OBSERVABLY we have ,
and Δt is the inseparable time during which
these component actions occurred, then we see that, stress-wise, all the
"zero-vectors" in figure 13 are quite different in their
internal stresses, 4-space potentials, and internal substructures.
For the five "zero sum" vectors, OBSERVABLY we have
|
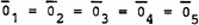
|
(31) |
whether or not
|
Δs3Δtm
= Δs3Δtn
(m ≠ n; 1 ≤ m ≤ 5; 1 ≤ n ≤
5) (32) |
But considering the substructures,
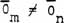 (1 ≤ m ≤ 5; 1 ≤ n ≤ 5; m ≠
n)
(33)
(1 ≤ m ≤ 5; 1 ≤ n ≤ 5; m ≠
n)
(33)
I now point out that a scalar can be regarded as a stressed zero-sum
vector, where the magnitude S of the scalar represents the internal
stress intensity caused by the substructure of the zero-vector.
Thus,
generally,
|
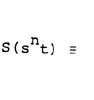 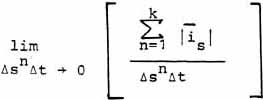
|
(34) |
That is, in general any observable scalar has, consists of, and is
comprised of a VIRTUAL (unobservable) substructure that is very real indeed.
One must also consider the scalar as existing for some finite time Δt, (at least for the time of one quantum change), and the intensity of the virtual actions occurring in the spatiotemporal substructure of the scalar during that time
Δt is proportional to the magnitude of the scalar.
Normally, the concept of a scalar
-- as presently used -- makes no allowance for the scalar to exist in time, or for a virtual vector
substructure, or for any patterning inside the substructure. This is equivalent to assuming that
and that all 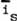 's
are evenly distributed. That is, from this new viewpoint, presently the
mathematical theory assumes all scalars to have an equal density of virtual
activity per spatiotemporal volume in its virtual substructure, and an isotropic
virtual pattern distribution of an infinite number of equal virtual vectors in
its 4-space substructure.28 's
are evenly distributed. That is, from this new viewpoint, presently the
mathematical theory assumes all scalars to have an equal density of virtual
activity per spatiotemporal volume in its virtual substructure, and an isotropic
virtual pattern distribution of an infinite number of equal virtual vectors in
its 4-space substructure.28
In the new
approach, neither of these two assumptions need hold -- though in special cases they can hold.
Thus present orthodox theory is
just a single special case of a more fundamental approach indicated here.
Note that, by
directly affecting and changing the virtual substructures of scalars and
vectors, we can directly perform virtual. state engineering, and this allows us
to directly "engineer" the so-called "laws of nature" of the
normal observable laboratory state and thus ENGINEER AND CHANGE PHYSICAL REALITY
ITSELF.29
In the new
approach, we can (observably) have
or
by the following means: In the first case (equation 36), we assume that the
virtual substructures are patterned, and interact nonlinearly in such a way as
to produce an extra observable. Thus we have a delta added to the normal
observable scalar results of the interaction, as follows:
|
2o + 2o = 4o +
Δv->o
|
(38) |
where subscript "o" means observable and "v" means virtual.
Note
that
indicates a delta due to virtual substructure interactions yielding an extra observable delta.
This extra delta may be either scalar or vector in
nature, depending on the circumstances and the particular interactions.
Note also that any
vector or scalar must now be considered to HAVE, CONTAIN, and CONSIST OF an
infinite substructure. And note that, similar to the scalar case, from the new
viewpoint the present theory assumes each scalar (point) of the vector to
have a structure similar to that of equation (34), except that now the scalars
are ordered, with a linearly decreasing internal stress density per unit scalar
along the line of the vector.
In the new
approach, vector interaction (superposition, for example) can now violate
present theory, if the two virtual substructures interact nonlinearly to produce
a nonzero, observable delta. Observably (macroscopically) , this delta,
again, may be either "scalar" or "vector."
This approach now becomes consistent with quantum mechanics at
the foundation level.
Next Page
|